The dictionary of basic mathematical notations in Mizar
Mizar Version: 7.0.05
MML Version: 4.09.842
C O N T E N T S
Logical notations
The notations of set theory
The notations of the sets of numbers
The notations for functions (relations)
The notations of arithmetic
The notations of numbers and special constants
The notations of elementary functions and complex numbers
The notations of limit and series
The notations of differentiation and integral
The notations of geometry
The notations of probability
The notations of vectors and matrices
[The way of description for entries in
the dictionary]
The way of description for entries in the dictionary is, in principle, as follows.
a usual mathematical notation English explanation of the notation [mizar] its corresponding mizar-notation (mizar-article: definition etc. in which the notation occurs) [usage] some example using the mizar-notation [the explanation of the mizar-example]
Logical notations
1. Κi`CP j negation [mizar] not (build in Mizar system)
[usage] not P [not P]
2. Θi&j and (conjunction) [mizar] & (build in Mizar system)
[usage] A & B [A and B]
3. Ι@or (disjunction) [mizar] or (build in Mizar system)
[usage] A or B [A or B]
4. ¨iΛC½jimplication [mizar] implies (build in Mizar system)
[usage] A implies B [A implies B]
5. Μ equivalence [mizar] iff (build in Mizar system)
[usage] A iff B [A is equivalent to B]
6. Ν for all [mizar] for (build in Mizar system)
[usage] 1. for a holds P [for every a, P holds.]
2. for a being set holds P [For every a which is a set, P holds.]
3. for a, b being set holds P [For every a, b which are sets, P holds.]
4. for a being set st P holds Q [For every set a satisfied with P, Q holds.]
7. Ξ@there exists [mizar] ex (build in Mizar system)
[usage] 1. ex a [There exists a.]
2. ex a st P [There exists a such that P holds.]
3. ex a being set st P [There exists a set a such that P holds.]
8. Ti1Ct C⊺ Ctrue, TRUEj truth [mizar] not contradiction (build in Mizar system)
[usage] A & not contradiction [A and TRUE]
TRUE (margrel:def 14)
[usage] TRUE = 1 [TRUE is equal to 1.]
9. F i0Cf CΫ Cfalsum, FALSEjfalsity, falsum [mizar] contradiction (build in Mizar system)
[usage] A implies contradiction [A implies FALSE]
FALSE (margrel:def 13)
[usage] FALSE = 0 [FALSE is equal to 0.]
The notations of set theory
1. Έ@element (of set) [mizar] in (hidden:pred 1)
[usage] a in b [a is an element of b: a belongs to b.]
2. = equality (of set) [mizar] = (hidden:pred 2)
[usage] a = b [a is equal to b.]
3. @the negation of equality (of set) [mizar] <> (hidden:prednot 2)
[usage] a <> b [a is not equal to b.]
4. { , } finite set with elements [mizar] { , } (tarski :def 1, etc.)
[usage] {a} [set with an element a.]; {a, b} [set with elements a, b], etc.
5. Ί@relation of inclusion (of set) [mizar] c= (tarski:def 3)
[usage] a c= b [a is included in b: b includes a: a is a subset of b.]
6. Ύ@union (of set) [mizar] union (tarski:def 3)
[usage] union a [the union of a]
7. Ώ intersection (of set) [mizar] meet (setfam_1:def 1)
[usage] meet a [the meet of a]
7. [ , ] ordered pair [mizar] [ , ] (tarski:def 5)
[usage] [a, b] [the ordered pair of a and b]
8. ∅ empty set [mizar] { } (xbool_0:def 1)
[usage] { } [{ } has no element.]
9. Ύ union (of two sets) [mizar] \/ (xbool_0:def 2)
[usage] a \/ b [the union of a and b]
10. Ώ intersection (of two sets) [mizar] /\ (xbool_0:def 3)
[usage] a /\ b [the intersection of a and b]
11. _@difference (of two sets) [mizar] \ (xbool_0:def 4)
[usage] a \ b [the set { x : x is an element of a and x is not an element of b}]
12. Ό@relation of proper subset( of set) [mizar] c< (xbool_0:def 8)
[usage] a c< b [a is a proper subset of b]
13. ( ) ci P j complement (of set) [mizar] ` (subset_1:def 5)
[usage] a ` [the complement of a]
14. ~@direct product of (sets) [mizar] [:,:] (zfmisc_1:defs 3)
[usage] [:a, b:] [the direct product of a and b];
[:a, b, c:] [the direct product of a, b and c], etc.
15. P ( ) power set (of set) [mizar] bool (zfmisc_1:def 1)
[usage] bool a [the power set of a]
16. { x : P } the set of elements x such that P holds ) [mizar] { x : P } (build in Mizar system)
[usage] 1. { x : P } [the set of elements x such that P holds]
2. { x where P : Q} [the set of element x satisfied with P such that Q holds]
The notations of the sets of numbers
1. N the set of natural numbers with 0 [mizar] NAT (numbers:funcnod 1); omega (ordinal2:def 5)
[usage] 0 in NAT [0 is an element of N.]
2. Z the set of integers [mizar] INT (numbers:def 4)
[usage] NAT c= INT [N is a subset of Z.]
3. Q the set of rational numbers [mizar] RAT (numbers:def 3)
[usage] NAT c= RAT [N is a subset of Q.]
4. R the set of real numbers [mizar] REAL (numbers:def 1)
[usage] RAT c= REAL [Q is a subset of R.]
5. C the set of complex numbers [mizar] COMPLEX (numbers:def 2)
[usage] REAL c= COMPLEX [R is a subset of C.]
6. On the set of ordinals [mizar] On (ordinal2:def 2)
[usage] omega c= On [Φ is a subset of On.]
7. Φ@the least set of limit ordinals [mizar] omega (ordinal2:def 5)
[usage] 0 in omega [0 is an element of Φ.]
The notations for functions (relations)
1. dom domain (of function (relation)) [mizar] dom (relat_1:def 4)
[usage] dom f [dom f is the domain of f.]
2. im (rng) range (of function (relation)) [mizar] rng (relat_1:def 5)
[usage] rng f [rng f is the range of f.]
1. ( )|1@inverse (of relation) [mizar] ~ (relat_1:def 7)
[usage] r ~ [r ~ is the inverse relation of r.]
2. ( )|1@inverse (of function) [mizar] " (relat_1:def 14)
[usage] f " [f " is the inverse relation of f.]
3. ∘@composition (of function (relation)) [mizar] * (relat_1:def 8)
[usage] f * g [f * g is the composition of f and g.]
6. 1/f the reciprocal of function f [mizar] ^ (rfunct_1:def 8)
[usage] f ^ [f ^ is the reciprocal of function f , that is, for every x, (f^)(x)=1/(f.x).]
7. aEf (af) scalar product of a scalar a and a real function f [mizar] a (#) f (seq_1:def 5); a g f (seq_1:def 5);
[usage] (a (#) f) .b = a * (f.b) [ (af)(b) = a(f(b) ) ];
(a g f) .b = a * (f.b) [ (af)(b) = a(f(b) ) ]
1. + addition of functions [mizar] + (seq_1:def 3)
[usage] f + g [f + g is addition of functions, that is , for every x, (f + g)(x) = f(x) +g(x).]
2. | subtraction of functions [mizar] - (seq_1:def 4)
[usage] f - g [f - g is subtraction of functions, that is , for every x, (f - g)(x) = f(x) - g(x).]
3. E multiplication of functions [mizar] (#) (seq_1:def 1)
[usage] f (#) g [f (#) g is product of functions, that is , for every x, (f (#) g )(x) = f(x)Eg(x).]
4. f/g fraction of functions [mizar] / (rfunct_1:def 4)
[usage] f/g [f/g is fraction of functions, that is , for every x, (f/g)(x)=(f(x)/g(x)).]
5. | the inverse of function with respect to addition [mizar] - (seq_1:def 7)
[usage] - f [ -f is inverse of function with respect to addition, that is , for every x, (-f )(x) = -f(x) .]
13. | restriction (of function (relation)) [mizar] | (relat_1:def 11)
[usage] f | a [f | a is the restriction of f with respect to a.]
14. f (a) image of a value a (with respect to function (relation) f ) [mizar] f.a (funct_1:def 4)
[usage] f.a [f.a is the image of a with respect to f.]
15. f (A) image of set A of values (with respect to function (relation) f ) [mizar] f .: A (relat_1:def 13)
[usage] f.:A [f.:A is the image of set A of values with respect to f.]
16. Hom(X, Y) the set of functions with domain X and range Y [mizar] Funcs( , ) (funct_2:def 2)
[usage] f in Funcs(X, Y) implies rng f = Y [(f is an element of Hom(X, Y)) implies rng f = Y.]
The notations of arithmetic
1. + addition [mizar] + (xcmplx_0:def 4)
[usage] a + b [a + b is the sum of a and b.]
2. E i~j multiplication [mizar] * (xcmplx_0:def 5)
[usage] a * b [a * b is the product of a and b.]
3. | subtraction [mizar] - (xcmplx_0:def 8)
[usage] a - b [a - b is the difference of a and b.]
4. | negative sign (minus sign) [mizar] - (xcmplx_0:def 6)
[usage] - a [-a is a negative number.]
5. / fraction [mizar] / (xcmplx_0:def 9)
[usage] a / b [a / b is a fraction with numerator a and denominator b.]
6. 1/a the reciprocal (number) of a [mizar] " (xcmplx_0:def 7)
[usage] a" [a" is the reciprocal (number) of a, that is 1/a.]
7. division [mizar] div (int_1:def 7)
[usage] a div b [a div b is the quotient when b devides a.]
6. mod residue [mizar] mod (int_1:def 8)
[usage] a mod b [a mod b is the remainder when b devides a.]
7. |@devides [mizar] devides (int_1:def 9)
[usage] a | b [a | b means that a devides b.]
8. lcm the least common multiple (of two natural numbers) [mizar] lcm (nat_1:def 4
[usage] a lcm b [a lcm b is the least common multiple of a and b.]
11. lcm the least common multiple (of two integers) [mizar] lcmf (int_2:def 2
[usage] a lcmf b [a lcm b is the least common multiple of |a| and |b|.]
12. gcd the greatest common divisor of two natural numbers) [mizar] hcf (nat_1:def 5)
[usage] a hcf b [a gcd b is the greatest common divisorof a and b.]
13. gcd the greatest common divisor (of two integers) [mizar] gcd (nat_1:def 5)
[usage] a gcd b [a gcd b is the greatest common divisor of |a| and |b|.]
14. e successor function [mizar] succ (ordinal1:def 1)
[usage] succ a [succ a is the successor of a]
15. inequality with equality [mizar] <= (xreal_0:def 2)
[usage] 1 <= 2 [1 is smaller than 2.]
16. inequality [mizar] > (xreal_0: prednot 4)
[usage] 2 > 1 [2 is larger than 1.]
17. inequality with equality [mizar] => (xreal_0:prednot 2)
[usage] 2 => 1 [2 is larger than 1.]
18. inequality [mizar] < (xreal_0:prednot 2)
[usage] 1 < 2 [1 is smaller than 2.]
19. min minimum [mizar] min (extreal2:def 1)
[usage] min(2,3) = 2 [2 is minimum with respect to 2 and 3.]
20. max maximum [mizar] max (extreal2:def 2)
[usage] max(2,3) = 3 [3 is maximum with respect to 2 and 3.]
21. ! factorial (of a natural number) [mizar] ! (sin_cos:def 30)
[usage] a ! [a ! is the factorial of a natural number a]
20. [ ]@Gaussf symbol [mizar] [\ /] (int_1:def 4)
[usage] [\ a/] [[\ a/] is [a].v
21. a ί b (mod c) a and b are congruent modulo c [mizar] , are_congruent_mod (int_1:def 3)
[usage] a , b are_congruent_mod c [(a , b are_congruent_mod c) means (a ί b (mod c) )]
The notations of numbers and special constants
1. 0 numeral zero [mizar] 0
2. 1 numeral one [mizar] 1 ; one (ordinal2:def 2)
3. 2 numeral two [mizar] 2
4. 3 numeral three [mizar] 3
5. 4 numeral four [mizar] 4
6. 5 numeral five [mizar] 5
7. 6 numeral six [mizar] 6
8. 7 numeral seven [mizar] 7
9. 8 numeral eight [mizar] 8
10. 9 numeral nine [mizar] 9
11. Ξ circle ratio [mizar] PI (sin_cos:def 30)
[usage] 3 < PI [Ξis greater than 3.]
12. e Napierfs number [mizar] number_e (power:def 4)
[usage] 2 < number_e [e is greater than 2.]
13. i imaginary number [mizar] <i> (xcmplx_0:def 1)
14. @infinity [mizar] +infty (supinf_1:def 1) or –infty (supinf_1:def 3)
15. + infinity [mizar] +infty (supinf_1:def 1)
16. |@infinity [mizar] –infty (supinf_1:def 3)
The notations for elementary functions and complex numbers
1. sin [mizar] sin (sin_cos:def 30)
[usage] sin a [the sine of a.]
2. cos [mizar] cos (sin_cos:def 22)
[usage] cos a [the cosine of a.]
3. tan [mizar] tan (sin_cos4:def 1)
[usage] tan a [the tangent of a.]
4. sec [mizar] sec (sin_cos4:def 4)
[usage] sec a [the second of a.]
5. cot [mizar] cot (sin_cos4:def 2)
[usage] cot a [the cotangent of a.]
6. arcsin [mizar] arcsin (sin_cos6:def 1)
[usage] arcsin a [the arcsine of a.]
7. arccos [mizar] arccos (sin_cos6:def 3)
[usage] arccos [the arccosine of a.]
8. ex exponential function (of real values) [mizar] exp (sin_cos:def 26)
[usage] exp x [the exponential function of x]
9. Re the real part of a complex number [mizar] Re (complex1:dfs 1)
[usage] Re a [the real part of a complex number a]
10. Im the imaginary part of a complex number [mizar] Im (complex1:dfs 2)
[usage] Im a [the imaginary part of a complex number a]
11. γ@positive square root (of a real number) [mizar] sqrt (square_1:def 4)
[usage] sqrt a [the square root of a]
12. nγ positive n-powered root (of a real number) [mizar] n-Root (prepower:def 3)
[usage] 3 -Root a [the positive cubic root of a]
13. ( ) 2 squre (of a number) [mizar] ^2 (square_1:def 3)
[usage] a^2 [the square of a]
14. ( ) 2 squre (of a number) [mizar] sqr are_1:def 3)
[usage] a^2 [the square of a]
15. ab a real number with exponent of a natural number [mizar] |^ (newton:def 1)
[usage] a |^ b [the b times power of real number a]
16. ab a real number with exponent of an integer [mizar] #Z (prepower:def 4)
[usage] a #Z b [the b times power of real number a]
17. ab a real number with exponent of a rational namber [mizar] #Q (prepower:def 5)
[usage] a #Q b [the b power of real number a]
18. ab a real number with exponent of a real number [mizar] #R (prepower:def 8)
[usage] a #R b [the b power of real number a]
19. ab a real number with exponent of a real number [mizar] to_power (power:def 2)
[usage] a to_power b [the b power of real number a]
20. | | absolute value (of a complex number) [mizar] abs (complex1:func 18)
[usage] abs a [the absolute value of a]
21. P@conjugate complex number (of complex number) [mizar] *f (complex1:def 15)
[usage] <i>*f [<i>*f = |<i>]
22. log logarithm [mizar] log( , ) (power:def 3)
[usage] log(a,b) [log(a,b) is a logarithm with base of logarithm a and anti-logarithm b.]
23. a + bi a complex number with its real part a and its imaginary part b ), where a and b are real numbers [mizar] [*a,b*] (arytm_0:def 7)
[usage] for a being Element of REAL holds [*a,0*] in REAL [It means that for aΈRCa+0iΈR holds.]
24. arg the argument of a complex number [mizar] Arg (comptrig:def 1)
[usage] Arg a [Arg a is the argument of a complex number a.]
The notations for limit and series
1. lim limit of complex sequence [mizar] lim (comseq_2:def 5)
[usage] 1. lim a [the limit of complex sequence a]
2. lim (a+b) = lim a + lim b [This holds if a and b are convergent.]
2. @pertial sum of a real sequence [mizar] Percial_Sums (series_1:def 1)
[usage] Percial_Sums a [pertial sum of real sequence a]
3. @sum of infinite series [mizar] Sum (series_1:def 3)
[usage] 1. Sums a [sum of infinite series of a real sequence a]
2. Sums a = lim Percial_Sums a [The sum of infinite series of a real sequence a is equal to the limit of the pertial sum of it.]
4. ¨+@(for a real sequence) divergent to the plus infinity [mizar] (is) divergent_to+infty (limfunc1:def 4)
[usage] a is divergent_to+infty [The real sequence a is divergent to the plus infinity, that is , a ¨+.]
5. ¨|@(for a real sequence) divergent to the minus infinity [mizar] (is) divergent_to-infty (limfunc1:def 5)
[usage] a is divergent_to-infty [The real sequence a is divergent to the minus infinity, that is , a ¨|.]
6.
![]() limit b of a real functionix ¨ a j [mizar]@lim( , )
(limfunc3: def 4)
limit b of a real functionix ¨ a j [mizar]@lim( , )
(limfunc3: def 4)
[usage] lim(f ,a) = b [f is convergent to b in a.]
7.
![]() limit b of a real functionix ¨ a + 0 j [mizar]@lim_right( , ) (limfunc2: def 8)
limit b of a real functionix ¨ a + 0 j [mizar]@lim_right( , ) (limfunc2: def 8)
[usage] lim_right(f ,a) = b [f is right-convergent to b in a.]
8.
![]() limit b of a real functionix ¨ a | 0 j [mizar]@lim_left( , ) (limfunc2: def 7)
limit b of a real functionix ¨ a | 0 j [mizar]@lim_left( , ) (limfunc2: def 7)
[usage] lim_left(f ,a) = b [f is left-convergent to b in a.]
9.
![]() a
real function f is divergent to +ix ¨ aj [mizar] is_divergent_to+infty_in (limfunc3: def 2)
a
real function f is divergent to +ix ¨ aj [mizar] is_divergent_to+infty_in (limfunc3: def 2)
[usage] f is_divergent_to+infty_in a [f is divergent to + in a.]
10.
![]() a
real function f is divergent to |ix ¨ aj [mizar] is_divergent_to-infty_in (limfunc3:
def 3)
a
real function f is divergent to |ix ¨ aj [mizar] is_divergent_to-infty_in (limfunc3:
def 3)
[usage] f is_divergent_to-infty_in a [f is divergent to | in a.]
11.
![]() a real function f is divergent to +ix ¨ a + 0 j [mizar]
is_right_divergent_to+infty_in
(limfunc2:def 5)
a real function f is divergent to +ix ¨ a + 0 j [mizar]
is_right_divergent_to+infty_in
(limfunc2:def 5)
[usage] f is_ right_divergent_to+infty_in a [f is right-divergent to + in a.]
12.
![]() a real function f is divergent to |ix ¨ a + 0 j [mizar]
is_right_divergent_to-infty_in
(limfunc2:def 6)
a real function f is divergent to |ix ¨ a + 0 j [mizar]
is_right_divergent_to-infty_in
(limfunc2:def 6)
[usage] f is_ right_divergent_to-infty_in a [f is right-divergent to | in a.]
13.
![]() a real function f is divergent to +ix ¨ a | 0 j [mizar] is_left_divergent_to+infty_in (limfunc2:def 2)
a real function f is divergent to +ix ¨ a | 0 j [mizar] is_left_divergent_to+infty_in (limfunc2:def 2)
[usage] f is_ left_divergent_to+infty_in a [f is left-divergent to + in a.]
14.
![]() a real function f is divergent to |ix ¨ a | 0 j [mizar] is_left_divergent_to-infty_in (limfunc2:def 3)
a real function f is divergent to |ix ¨ a | 0 j [mizar] is_left_divergent_to-infty_in (limfunc2:def 3)
[usage] f is_ left_divergent_to-infty_in a [f is left-divergent to | in a.]
15.
![]() limit of a real functionix ¨ + j [mizar] lim_in+infty
(limfunc1:def 12)
limit of a real functionix ¨ + j [mizar] lim_in+infty
(limfunc1:def 12)
[usage] lim_in+infty f = a [the limit a of a real function f in the plus infinity]
16.
![]() limit of a real functionix ¨ | j [mizar] lim_in-infty (limfunc1:def 13)
limit of a real functionix ¨ | j [mizar] lim_in-infty (limfunc1:def 13)
[usage] lim_in-infty f = a [the limit a of a real function f in the minus infinity]
17.
![]() (for
a real function) divergent to the plus infinity (x ¨+) [mizar] (is) divergent_in+infty_to-infty (limfunc1:def 7)
(for
a real function) divergent to the plus infinity (x ¨+) [mizar] (is) divergent_in+infty_to-infty (limfunc1:def 7)
[usage] f is divergent_in+infty_to-infty [The real function f is divergent to the plus infinity when x ¨+.]
18.
![]() (for
a real function) divergent to the minus infinity (x ¨+) [mizar] (is) divergent_in+infty_to-infty (limfunc1:def 8)
(for
a real function) divergent to the minus infinity (x ¨+) [mizar] (is) divergent_in+infty_to-infty (limfunc1:def 8)
[usage] f is divergent_in+infty_to-infty [The real function f is divergent to the minus infinity when x ¨+.]
19.
![]() (for a real function) divergent to the
plus infinity (x ¨|)
[mizar] (is)
divergent_in-infty_to+infty
(limfunc1:def 10)
(for a real function) divergent to the
plus infinity (x ¨|)
[mizar] (is)
divergent_in-infty_to+infty
(limfunc1:def 10)
[usage] f is divergent_in-infty_to+infty [The real function f is divergent to the plus infinity when x ¨|.]
20.
![]() (for
a real function) divergent to the minus infinity (x ¨|) [mizar] (is) divergent_in-infty_to-infty (limfunc1:def 11)
(for
a real function) divergent to the minus infinity (x ¨|) [mizar] (is) divergent_in-infty_to-infty (limfunc1:def 11)
[usage] f is divergent_in-infty_to-infty [The real function f is divergent to the minus infinity when x ¨|.]
The notations for differentiation and integral
1. ( , ) open interval [mizar] ]. , .[ (rcomp_1:def 2)
[usage] ].0 , 1.[ [This is the open interval between 0 and 1.]
2. ] , [ open interval [mizar] ]. , .[ (rcomp_1:def 2)
[usage] ].0 , 1.[ [This is the open interval between 0 and 1.]
3. ff(a) differential coefficient of real function f in a [mizar] diff(f, a) (fdiff_1:def 6)
[usage] diff(f + g, a) = diff(f, a) + diff(g, a) [This means (f + g)f (a) = ff (a) + gf(a) ]
4. f e (x) (xΈa) the differential of a real function f differentiable on a Ί R [mizar] f `|a (fdiff_1:def 8)
[usage] f `|REAL [This is the differential of the real function f differentiable on R.]
5. f e the differential of a real function f differentiable on R [mizar] f `|REAL (fdiff_1:def 8)
[usage] (f `|REAL).a [This is the differential coefficient of the real function f in a .]
6.
![]() @indefinite Riemann integral of a real
function [mizar] integral [integra1:def 18]
@indefinite Riemann integral of a real
function [mizar] integral [integra1:def 18]
The notations for geometry
1. AB line through A and B in 3 dimentional Euclidian space [mizar] Line( , ) (euclid_1:def 1)
[usage] 1. Line(A,B) st A, B in REAL 3 [line through A and B in 3 dimentional Euclidian space, where A, B are real 3-tuples.]
2. for A, B st A, B in REAL 3 holds Line(A,B) = Line(B,A) [line through A and B is equal to line through B and A.]
The notations for probability
1. Pr probability [mizar] Probability (of ) (prob_1:def 13)
[usage] Probability of X [This means Pr(X), that is, the probability of an event X.]
The notations for vectors and matrices
1. A is an n~m matrix over R [mizar] A is Matrix of n,m,REAL (matrix_1: def 3)
2. A is an n~m matrix over C [mizar] A is Matrix of n,m,COMPLEX (matrix_1: def 3)
3.
![]() 1~c matrix a (line
vector) [mizar] <*a*> (matrix_1:11)
1~c matrix a (line
vector) [mizar] <*a*> (matrix_1:11)
4.
![]() 1~ matrix a (line
vector) [mizar] <*a*> st width <*a*> = n
(matrix_1:11; matrix_1: def 4)
1~ matrix a (line
vector) [mizar] <*a*> st width <*a*> = n
(matrix_1:11; matrix_1: def 4)
4.
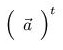 c~1 matrix a
(column vector) [mizar] <*a*>@ (matrix_1:11; matrix_1: def 7 )
c~1 matrix a
(column vector) [mizar] <*a*>@ (matrix_1:11; matrix_1: def 7 )
5.
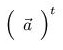 n~1 matrix a (column vector) [mizar] <*a*>@ st width <*a*> =
n (matrix_1:11; matrix_1: def 7 )
n~1 matrix a (column vector) [mizar] <*a*>@ st width <*a*> =
n (matrix_1:11; matrix_1: def 7 )
6.
 2~c matrix [mizar] <*a,b*> (matrix_1:12)
2~c matrix [mizar] <*a,b*> (matrix_1:12)
7.
 2~n matrix [mizar] <*a,b*> st width <*a,b*> = n
(matrix_1:12; matrix_1: def 4)
2~n matrix [mizar] <*a,b*> st width <*a,b*> = n
(matrix_1:12; matrix_1: def 4)
8.
 c~2
matrix [mizar] <*a,b*>@ (matrix_1:12; matrix_1: def 7)
c~2
matrix [mizar] <*a,b*>@ (matrix_1:12; matrix_1: def 7)
9.
 ~2
matrix [mizar] <*a,b*>@ st width <*a*> = n
(matrix_1:12; matrix_1: def 7)
~2
matrix [mizar] <*a,b*>@ st width <*a*> = n
(matrix_1:12; matrix_1: def 7)
10.
![]() 1~1 matrix with element a
matrix [mizar] <*<*a*>*> (matrix_1:15)
1~1 matrix with element a
matrix [mizar] <*<*a*>*> (matrix_1:15)
11.
![]() 1~2 matrix with elements a and b [mizar] <*<*a*>,<*b*>*> (matrix_1:15)
1~2 matrix with elements a and b [mizar] <*<*a*>,<*b*>*> (matrix_1:15)
12.
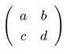 2~2 matrix with elements a, b, c and d [mizar]
<*<*a,b*>,<*c,d*>*> (matrix_1:15)
2~2 matrix with elements a, b, c and d [mizar]
<*<*a,b*>,<*c,d*>*> (matrix_1:15)
13.
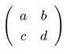 2~2 matrix with elements a, b, c and d [mizar] (a,b)][(b,c) (matrix_2:def 2)
2~2 matrix with elements a, b, c and d [mizar] (a,b)][(b,c) (matrix_2:def 2)
14.
![]() (i, j)-element of a matrix a [mizar] A*(i,j) (matrix_1:def 6)
(i, j)-element of a matrix a [mizar] A*(i,j) (matrix_1:def 6)
15. At transposed matrix of A [mizar] @ (matrix_1:def 7)
[usage] A@ [A@ is the transposed matrix of A.]
16. + addition of matrices [mizar] + (matrix_1:def 7)
[usage] a + b [the sum of matrices a and b]
17. | minus sign of matrix matrices [mizar] - (matrix_1:def 13)
[usage] -a [the inverse of a matrix a with resprect to addition]
18. E (~@or nothing) multiplication of matrices [mizar] * (matrix_3:def 4)
[usage] a * b [the product of matrices a and b]
19. ( , ) ( < , > ) the inner product of finite sequences recognized as vectors [mizar] g*h (fvsum_1:def 10)
[usage] ag*hb [the inner product of finite sequences a and b recognized as vectors]
20. the n-th line of a matrix a [mizar] Line(a,n) (matrix_1:def 8)
21. the n-th colum of a
matrix a [mizar]
22. O n~m zero matrix [mizar] 0.(n,m) (matrix_1:def 11)
23. E ( I ) n~n unit matrix [mizar] 1.(n,m) (matrix_1:def 12)
24. det a the determinant of a matrix a [mizar] Det (matrix_1:def 12)
[usage] Det a [the determinant of a matrix a]