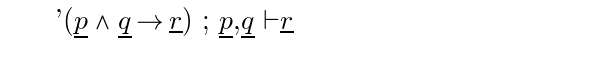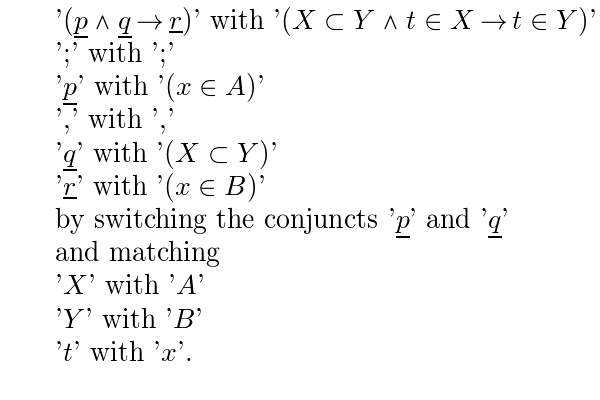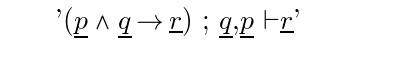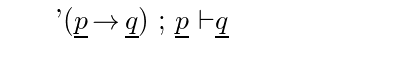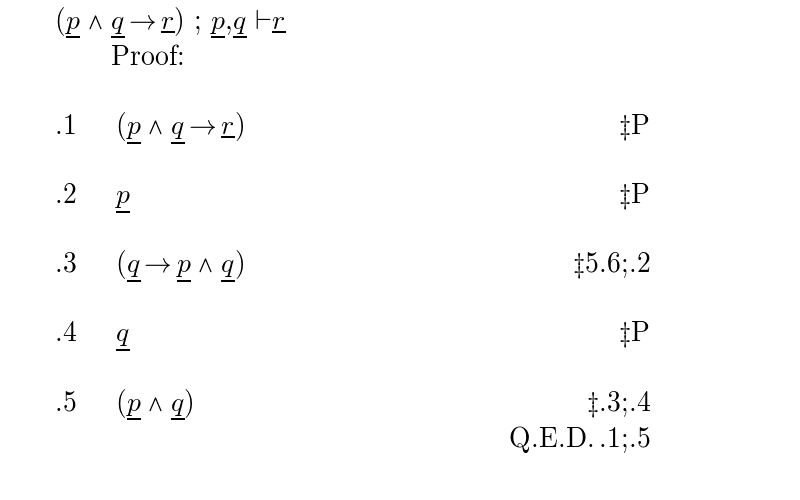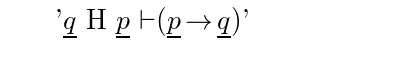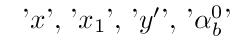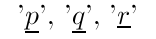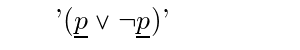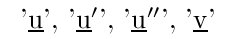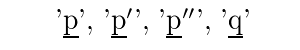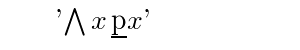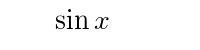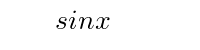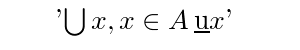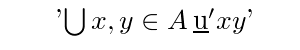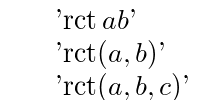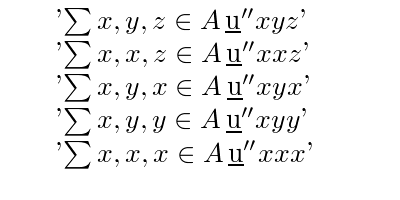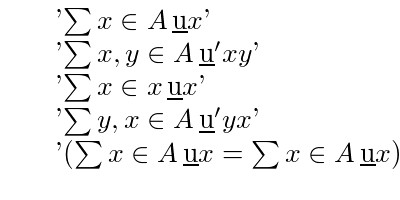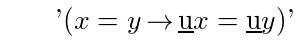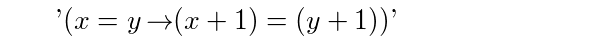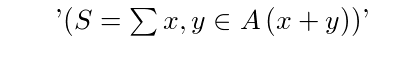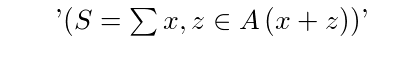ProofCheck Manual
A. Commands
ProofCheck is run using commands from the command line in any system that has Python 3 installed. The most important commands are parse and check. The commands renum and renote are also very useful while writing documents for ProofCheck.
1. parse <source-filename>
parse operates on TeX files containing ordinary text and mathematics presented using TeX or LaTeX. parse will attempt to parse everything in the file that is in TeX's math mode. The program will stop running and return an error message whenever it encounters a line of math that cannot be parsed. If proofs are included in the file and parse finds no errors it creates a file of parsed proofs which is used by check.
Any math expression numbered using the "\prop" macro is taken as a proposition. A proof is either a simple justification or a sequence of math expressions marked as notes, using the "\note" macro, together with justifications marked using the "\By" macro, and terminated by a QED, indicated with the "\Bye" macro. If a proposition is followed by a proof then parse attempts to parse the proof as well as the proposition. parse halts when it encounters a math expression or a proof which it cannot parse. Any new definitions encountered are reported as well as the number of proofs, old definitions, and unproved propositions. If no errors are found the parsed propositions and proofs are stored in a ".pfs" file for the use of check. Because new definitions are parsed differently from old definitions, it is sometimes necessary to run parse two times before check can succeed.
In math-only mode parse ignores proof structuring and just tries to parse each TeX math expression. It halts when it encounters an expression that it cannot parse. It uses syntax information stored in the ".dfs" file to do the parse. Any new definitions encountered are reported and the updated information is stored in the ".dfs" file.
The following optional switches may be placed anywhere on the command line after the parse command.
-e expression Parse the expression given on the command line using the definitions in the source-file's ".dfs" file. -m Use math-only mode. Ignore proof structuring information. -q Use quiet mode. Suppress output. -r Rebuild the ".dfs" file. Expunge old definitions.
2. check <source-filename> <reference_number or pattern>
check goes through each of the identified proofs in the file, and returns an error message for any inference that it cannot confirm as checking.
check takes as a second parameter the number of a theorem whose proof is to be checked or the line number of a rule of inference whose derivation is to be checked. The second parameter may also be a Python regular expression.
The first parameter is the name of the file containing the proof or proofs to be checked.
Examples
check book 3.5checks the proof of theorem 3.5 in the file "book.tex"
check book 255checks the derivation of the rule of inference on line 255
check book [2-4]\\.checks all theorems in a file "book.tex" with numbers beginning "2." "3.", or "4.". Because a dot is used in regular expression patterns as a wild card the slash is necessary. Including the slashes prevents matches with theorems numbers such as "29.2", "45.6".
check book .checks all proofs and derivations in the file.
For each step of the proof of the specified theorem check searches the rules file for a rule of inference which justifies the step and if it succeeds prints out the line number of the first such rule found, and otherwise reports that the step does not check.
The following optional switches may be placed anywhere on the command line after the check command.
-c Display cases for debugging purposes. -i Display full text of each inference rule found. -l linenum Use only the rule with the specified line number. -m Report rules used in multi-line transitivity checks. -r rulesfile Use rules from the specified file. -t Trace premises for relevant logic. -v Display verbose output from the unifier.
3. renote <source-filename>
renumbers all the notes in each proof so as to make them consecutive. This allows an author to insert notes with out of sequence, haphazard or ad hoc numbering while a proof is still in development.
4. renum <source-filename>
renumbers all the propositions so that they are consistent with the chapter numbering (or section numbering in LaTeX). The renumbering applies to all references anywhere in the document. To avoid catching references to external documents in the renumbering the dot in these external references may be enclosed by braces: {.} renum also creates a time-stamped ".rnm" file with a map of the renumbering.
5. audit <source-filename> <theorem-number>
scans a source file for both dependencies upon, and dependencies of, a proposition in that file whose number is given as the second parameter. The theorem-number has the form num.num. Dependencies on rules of inference are not stored and therefore cannot be retrieved.
6. lsdfs <source-filename>
displays the information contained in the ".dfs" file associated with the file named by <source-filename> .
7. lspfs <source-filename>
displays the information contained in the ".pfs" file associated with the file named by <source-filename> .
8. lstrc <source-filename>
displays the information contained in the ".trc" file associated with the file named by <source-filename> .
B. Directives
The percent sign begins a TeX comment. ProofCheck directives use this feature to avoid display. The mathematical symbols or expressions occurring in ProofCheck directives must not be enclosed in TeX dollar signs.
A ProofCheck directive may be located in a source file or in the associated ".tdf" or ".ldf" file.
1. %term_definor: <symbol>
establishes the symbol to be used in definitions of terms as well as in assignment statements used in proofs.
2. %formula_definor: <symbol>
establishes the symbol to be used to define formulas.
3. %variable: <symbol>
Makes <symbol> into a mathematical variable. This can only be done if TeX treats it as a token.
4. %undefined_term: <math-expression>
is used when a term is to be taken as primitive, for whatever reason.
5. %undefined_formula: <math-expression>
is used when a formula is to be taken as primitive, for whatever reason.
6. %notarian_term: <math expression>
These expressions are similar to the notarian formulas. Summation, for example, is a bound variable term which can be handled using notarians:
Example
%notarian_term: \sum x ; \qbar x \ubar x
7. %notarian_formula: <math expression>
These expressions, codified by Morse, must begin with a unique constant and end with "x;" and two schematic expressions:
Example
%notarian_formula: \Some x ; \qbar x \pbar x
8 %speechpart: <infix-symbol-or-precedence-value> <kind>
Assigns a kind to infix operators, where <kind> may be verb, conjunction, or reset. These designations are used to parse the scope of notarian expressions.
9. %identity: <symbol>
Causes <symbol> to be passed over in the parse of multi-line notes involving transitivity. Thus a note of the form:
(a = b
< c)will create a goal (called a sigma goal)
(a < c)if = has been declared as an identity:
%identity: =
10. %set_precedence: <infix-symbol[s]> <number>
is used to assign a precedence value to an infix math-symbol.
Example: Suppose an author wanted to set up an infix operator \lessthan with a precedence value of 6 . The following assignment could be made:
%set_precedence: \lessthan 6This would allow for the infix usage of \lessthan.
A concatenation of infix symbols used as one is called a nexus. To use \lessthan = as a nexus of precedence 7 the following assignment suffices
%set_precedence: \lessthan = 7Symbols joined to form a nexus must singly have their own precedence values.
11. %def_precedence: <number> <checker> [<handler>]
associates to each numerical precedence value a checker which is a Python function which determines whether an infix expression, whose operators all have the given precedence, is valid. The optional handler is a re-write function.
12. %associative: <symbol> [<line-number>]
instructs the unifier to treat the (infix) symbol as an associative operator. If more than one symbol is given the combination is treated as a nexus. Different associative operators must be declared on different lines. At present the declaration is effective only in combination with the %commutative: declaration. The optional line number specifies the line at which the use of the associative assumption by the unifier begins.
13. %commutative: <symbol> [<line-number>]
instructs the unifier to treat the (infix) symbol as an commutiative operator. If more than one symbol is given the combination is treated as a nexus. Different commutiative operators must be declared on different lines. At present the declaration is effective only in combination with the %associative: declaration. The optional line number specifies the line at which the use of the commutiative assumption by the unifier begins.
14. %flanker: <symbol>
Creates a symbol which is parsed like the absolute value symbol. It is not the case that an introductor which occurs in a form other than at the beginning necessarily becomes a flanker.
15. %def_symbol: <user-symbol> <support-file-symbol>
allows an author to set up a symbol which will function as the equivalent of a symbol used in ProofCheck's default supporting files, such as the rules of inference or common notions files.
Example: The inverted letter 'A', written in TeX as '\forall', is generally used as the universal quantifier. The default rules of inference file uses an inverted 'V', written as '\Each'. To use '\forall' in documents an author may define:
%def_symbol: \forall \Each
16. %def_tracer: <line_number> <support-file-symbol>
In relevant logic, each rule of inference has an ancestor tracing rule. In ProofCheck these are stated using Python set operators. For derived rules of inference they are computed, but for primitive rules of inference they must be given.
Example if modus ponens occurs on line 43 of a logic development file. Then the associated ".tdf" file should contain the directive
%def_tracer: 43 (0 | 2)These directives are used by check to initialize the ".trc" file.
17. %external_ref: <suffix> <external-filename>
defines a short suffix to be appended to numerical theorem references which refer to theorems in files other than the one whose proof is being checked. The short suffix must consist of lower case letters.
Example: Suppose that an author needs to use Theorem 3.4 from a file "limits.tex." To set up the letter 'a' as an abbreviation for this external file the following definition could be used:
%external_ref: a limits.texThis would enable the author to invoke Theorem 3.4 in a proof using the reference "3.4a".
18. %refnum_format: <latex-sectioning-unit-propnum-pair>
is used with LaTeX to determine which LaTeX sectioning unit the major number of ProofCheck major.prop theorem number pairs should keep in step with. The default is section. The other possibilities are chapter, subsection, subsubsection, paragraph,etc. For example to make the reference numerals of propositions chapter.propnum use:
%refnum_format: chapter.propIn plain TeX the default is chapter.prop where chapters must be introduced with the marking: \chap <num, name, etc.>
19. %propnum_format: <latex-sectioning-unit-propnum-pair>
is used with LaTeX to determine which LaTeX sectioning units should be displayed along with the \prop label. It may be shorter than the refnum_format.
Using a shorter display form can cause information loss. To avoid this when using renum a copy of the file using refnum_format labelling should be created using the "-f" option, before edits are made which violate LaTeX section boundaries.
20. %rules_file: <rules-file-name>
specifies a file to be used as a source of inference rules. The directive may be used more than once thereby specifying more than one such file.
21. %reductions_file: <rules-file-name>
defines a file containing inference rules which are to be used as reductions. The directive may be used more than once thereby specifying more than one file.
22. %transitive: <rules-filename> [<line-number>-<line-number>]
establishes a file of rules of inference, or an optional range of lines in a file, as rules to be searched when transitivity steps in a multi-line note need justification.
C. TeX Files
Besides the source file other TeX files are needed in order for parse and check to work. Except for the TeX definition files they should all carry a ".tex" extension.
1. TeX Definition Files (.tdf or .ldf)
The primary purpose of the TeX definition files (or LaTeX definition files) is to contain TeX \def macros for the mathematical constant symbols the author needs to define. There are typically many of these macros and it avoids clutter to put them in a file separate from the TeX source file. Each TeX source file should have an identically named ".tdf" and each LaTeX source file should have an identically named ".ldf" file.
A TeX definition file should be invoked with an \input statement near the beginning of the source file. This file should also be used to store the Directives the author needs in order to customize the operation of ProofCheck.
When definitions contained in some other source file are implicitly relied upon, then its associated TeX definition file should be input as well.
One essential TeX definition file is utility.tdf (utility.ldf) The line
\input utility.tdfneeds to be one of the first statements in a source file containing proofs This file contains the TeX macros for Proof Structuring Notation macros needed to allow parse to run.
A source file will typically therefore have at least a few TeX definition files input at the beginning. Such files are a kind of header file.
2. Rules of Inference Files
Rules of Inference files are specified in one of the following three ways: If the -r switch on the check script is used the file whose name follows the switch becomes the file searched for inference rules.
If the %rules_file: directive is used, it may be used more than once. Each time it is used another file is added to the list of files searched for inference rules.
Example
%rules_file: rules.texIf neither of these options for specifying a rules of inference file is used then the source file itself is used. In this case only rules preceding an item being checked are allowed as search results. This makes sense in a logic development file.
In a rules of inference file any line having the format of a rule of inference is taken as a rule of inference. The format of a rule of inference is:
<mathematical formulas and reference constants> |- <goal>where the goal is another formula and the reference constants come the following list
( ) + , - : ; | U G H Sand the goal and other mathematical formulas are dollar delimited. Other lines are effectively comment lines. The modus ponens rule for example can be stated as follows:
$(\pvar \c \qvar)$;$\pvar$ \C $\qvar$which, assuming that '\c' codes for the implies sign, is TeX for
(p --> q) ; p |- qThe sole reference punctuator used in this rule is the semi-colon. A note can be justified by the modus ponens rule if it carries a justification such as:
\By 1.2;.3and the expression formed by the note followed by Theorem 1.2, the semi-colon, and note 3 can be unified with the modus ponens rule. In order for the unification to succeed Theorem 1.2 must have the form (p --> q) and where note 3 is p and the note being justified is q.
The punctuation in a justification must match that of the rule of inference it is to match exactly. The goal and the propositions referred to in the justification are matched against the corresponding formulas in the rule of inference and the unifier looks for a match. A different rule of inference file may be used if its name is supplied as the third parameter of check. Variables near the beginning of the alphabet in the list fixed_variables are fixed when given to the unifier and other variables must be replaced to match them (and not vice versa).
3. External Reference Files
Numerical references in proofs to theorems in external files are distinguished from references internal to the document in that they end with lower case letters or begin with a zero.
Examples
To set up the file morse.tex as the file referred to by references ending with ap the following directive is used:
%external_ref: ap morse.texThus a reference to 4.72ap refers to theorem 4.72 in the file morse.tex To set up the file common.tex as the file referred to by references beginning with zero the following directive is used:
%external_ref: 0 common.texThus a reference to 03.56 refers to theorem 3.56 in the file common.tex
Given that references from this file are used in proof its notation needs to be understood by check. Consequently its TeX definition needs to be input at the top. When a ".dfs" file is initialized it is merged from the ".dfs" files associated with all the included ".tdf" (or ".ldf") files.
3. Logic Development Files
In logic development files, theorems are proved and rules of inference are derived, in the same file. Derivations of rules of inference are sequences of steps which form a template for replacing the use of a derived rule in a proof with steps not using the rule. Proofs and derivations may depend only on previously established theorems and rules of inference. Primitive rules, rules which cannot be derived, include not only rules like modus ponens, but also deduction theorems which can be used as rules of inference, both primitive and derived. External references are not used.
The purpose of these files is to close the gap introduced by using rules of inference files containing a large number (over a thousand) rules of inference. When these are introduced manually errors inevitably intrude. Logic development files are also usefully in developing non-standard logics such as constructive logic or relevant logic which can be counter-intuitive.
D. Python Data Files
These files are Python pickle files and can be read if the output from the corresponding ProofCheck ls script is scrolled. Pickle files should not, of course, be directly edited by the user. Their names are the same as that of the source file except that the ".tex" extension is replaced by ".dfs", ".pfs", or ".trc".
1. .dfs File
This file records syntax information from the mathematical definitions contained in the source file as well as other information. It is initialized by running parse on the source file. It is a Python pickle file. The information in it is stored cumulatively. To "undo" a definition stored in the ".dfs" file parse should be run using the "-r" option.
2. .pfs File
This is a large file containing a parse of each propostion and proof found in the TeX source file. It is produced by parse and used by check.
3. .trc File
This file containing tracing information for rules of inference checked using the tracing option. It is produced by check and used by check, but only when the "-t" option is invoked.
E. Proof Syntax
There are two kinds of formal proofs checked, proofs of theorems, and proofs of derived rules of inference which will be called derivations to distinguish them from proofs of theorems.
1. Notes
Proofs and derivations consist of notes, each with an optional justification, consisting of references to previous notes in the same proof, other theorems in the same file, or theorems in an external file, separated by reference constants. All theorems and notes used in a justification must be given explicitly since for them, no searching is done. Rules of inference on the other hand do not need explicit reference in a justification since check does a search for an inference rule to match each justification.
References to previous notes use a .num format where the num is the numerical tag attached to a previous note using the \note notation.
References to other theorems in the same file use a num.num format. This format may be altered using a %refnum_format: declaration. It is the same as the numerical tag attached to the theorem itself using the \prop notation unless this is altered using the %propnum_format: declaration.
References to theorems in external files attach to the theorem numeration either a prefixed zero or suffixed lower case letters. These conventions are set up using the %external_ref: declaration.
The following symbols, the reference constants, are used as punctuation separating the numerical tags in a justification.
( ) + , - : ; | U G H S PExample: Suppose that we have a note:
'\note 5 $(x \in B)$ \By 2.5;.2,.3'This note would make sense if there were a previous theorem 2.5 such as:
'\prop 2.5 $(X \subset Y \And t \in X \c t \in Y)$'where '\in' refers to elementhood and '\c' logical implication, and there exist previous notes 2 and 3 such as:
'\note 2 $(x \in A)$ '
'\note 3 $(A \subset B)$ '
To check this note the list of rules of inference are searched to find a match.
2. Rules of Inference
Although rules of inference dealing with subsitution, and subsumed under unification, are stated in the meta-language, and not part of the same formal language as the mathematics, most rules of inference used in ProofCheck statements in the formal language wheither primitive like axioms, or derived rules which are provable from the primitive rules. Each rule of inference is a line consisting of two parts, the premises punctuated by reference constants, and the conclusion separated by a '\C' which appears as:
.
The rule of inference needed to match the note 5 given in the example above is:
'$(\pvar \And \qvar \c \rvar)$;$\pvar$,$\qvar$\C$\rvar$which appears as:
If this rule is located then the note will be checked because the unifier will match
Reference consonants must match. The equivalence of (\pvar \And \qvar) is recognized assuming that '\And' has been declared both commutative and associative. If this has not been done then in the rules files so far constructed the convention has been observed that all permutations of comma operands are stored. Hence there should also be a rule:
If we assume that the following rule, modus ponens, has already been stated:
and that there is a theorem 5.6: '$(\pvar \c (\qvar \c (\pvar \And \qvar)))$' then we may state and prove the above rule as follows:
Notes 1, 2, and 4 are justified with the reference constant 'P' for premise which is used only in derivations. Notes 3,5 and the QED all check using modus ponens, which does not need a reference since ProofCheck assumes responsibility for locating rules of inference.
3. Deductions
An intuitive way of showing that p implies q is to take p as a given and then prove q, based on that assumption. In standard logic this is a valid procedure, justified by the deduction theorem. The deduction theorem can be formulated as a rule of inference as follows:
'$\qvar$ H $\pvar$ \C $(\pvar \c \qvar)$'where the $\pvar$ note or notes immediately following the reference constant, 'H' which stands for "Hence", must be justified by the reference constant 'G' which stands for "Given." It appears as:
The notes from the Given to the Hence form a deduction. Within this deduction any variables introduced in the Given note become fixed in the sense that substitution rules of inference must treat them as constants, not variables. The notes of the deduction, up until the last line justified by the Hence rule, may not be referenced from outside the deduction.
4. Proof Structuring Notation
a. \By <reference-expressions and reference-punctuators>
is the general form of most justifications. For more on justifications see Justifications
b. \Bye <reference-expressions and reference-punctuators>
signals the end of a proof. It is rendered with a QED. A justification beginning with \Bye is similar to an regular \By justification except that the justificand, or item being justified, is no longer given following a \note but is omitted as understood. If a theorem is proved then the statement of the theorem itself is the justificand. If rule of inference is derived then the justificand is the conclusion of the rule, (the expression following the '\C').
c. \chap {<num>. <chapter-title >}
is used for chapter titles in a TeX file. In a LaTeX file, LaTeX section headers are used instead. Proposition numbers are arranged according to the chapter (or section numbers). The author need not enter these numbers consecutively since renum will renumber chapters and propositions so as to make them consecutive.
d. \linea, \lineb, \linec,..., \linez
These are the line indentation macros. The first seven of these 26 macros produce a line break followed by a prescribed indentation, 20 points for \linea, 40 points for \lineb, 60 points for \linec, etc. The others may be defined as needed by the author.
TeX takes expressions enclosed in dollar signs as mathematical expressions. Syntactically complete terms or formulas are sometimes too long to be conveniently handled as single TeX math expressions. ProofCheck allows complete terms or formulas to be broken into pieces provided these pieces are separated only by white space, these line indentation macros, and in the case of multi-line notes, justifications.
e. \noparse
turns off the parser for the remainder of the line in which it occurs. This is useful since it is sometimes necessary to use mathematical symbols or notation out of context in a way that cannot be parsed.
f. \note <note-number> <note> [<justification>]
A note-number is any positive integer with a no more than four digit representation. It is rendered with an initial dot. The note is some mathematical assertion used in the proof. A justification begins with a \By macro.
g. \prop <proposition-number> <proposition> [<justification>]
Every definition, axiom, or theorem which needs to be referred to later must be introduced in this way. A theorem may be followed by a proof.
The proposition-number must take the form: num1.num2 where num1 is the chapter number (or section number in LaTeX)
The proposition must be enclosed in TeX dollar signs. It may be broken into more than one math expression so as to span multiple lines, only if these expressions are separated by line indentation macros.
F. Math Syntax
1. Kinds of Symbols
There are two kinds symbols: variables and constants.
There are two types of variables: term variables and formula variables, each of which may be of either the first order or the second order. By far the most common of these are the first order term variables, called object variables. The first order formula variables are called sentential variables. Following Morse, the second order variables are here called schemators. The term schemators are in essence function variables, and formula schemators in essence are predicate variables. When just variables are referred to it is object variables that are intended unless there is explicit qualification to the contrary.
a. Object Variables
The parser recognizes single Latin letters, LaTeX's Greek letters (except omega), and primed, subscripted and superscripted versions of these as object variables. The expressions '\p', '\pp', '\ppp', etc. are defined in ProofCheck using TeX macros to be the superscripted prime, double prime, triple prime, etc.
Examples of Variables:
'x', 'x_1', 'y\p', '\alpha^0_b'These appear as follows:
Other forms of decoration such as stars and overbars are not currently supported.
Symbols which would otherwise be recognized as constants may be used as variables if they are declared as such using the proofcheck directive:
%variable: <symbol>
b. Sentential Variables
Sentential variables are variables which range over sentences. In standard logic they are the Boolean variables. They are first order formula variables and are used to state theorems of logic and rules of inference.
Examples of Sentential Variables:
'\pvar', '\qvar', '\rvar',They are italicized and underlined Latin letters:
The law of the excluded middle, for example, is stated using sentential variables as follows:
$(\pvar \Or \Not \pvar)$It appears as:
c. Term Schemators
A schemator is a second order variable which is not quantified over. It may be either a term schemator or a formula schemator. Whether it is a term or a formula schemator it takes one or more terms as arguments. The number of these arguments is called the arity of the schemator. Term schemators use the letters 'u', 'v', and 'w' optionally followed by primes. They are underlined but not italicized:
Examples of term schemators
'\ubar', '\ubarp', '\ubarpp', '\vbar',They appear as:
The arity of the schemator is one more than the number of primes following it. The schemator '\ubar' has arity 1. Similarly '\ubarp' has arity 2, etc. A schematic expression is a schemator of arity n followed by n variables. Schematic expressions are used in definitions of terms or formulas that contain bound variables as well as in many in rules of inference. For example a form for indexed union is:
'\bigcup x \in A \ubar x'It appears as:
It denotes the union of all the \ubar x where x ranges over A.
d. Formula Schemators
Formula schemators are essentially the same as predicate variables,
Examples of formula schemators
'\pbar', '\pbarp', '\pbarpp', '\qbar',They appear as follows:
For example, the expression '\pbar x' represents a formula which at least potentially depends on x. Russell referred to such expressions as propositional functions. The use of explicitly second order expressions of this nature allows predicate logic to be stated without the use of schemes. For example the basic form for universal quantification is:
\Each x \pbar xIf it is rendered using the Polish quantifier it appears as follows:
e. Constants
A constant is any symbol which is not a variable or a schemator.
Although some constants are existing characters such as '+' and '=' most constants must be constructed using macros. TeX and especially LaTeX and AMS-TeX already have a large number of symbols defined by means of such macros. Examples of these are '\lt' for '<' and '\sin' for 'sin'. The macro for the sine in TeX's file, plain.tex, (except for a \nolimits qualifier) is
\def\sin{\mathop{\rm sin}}Because of this macro '\sin x' appears as:
whereas 'sin x' appears as:
Worse yet, ProofCheck's parser could then, assuming that when terms are writtenly adjacently multiplication is intended, interpret this expression as a product of the four variables 's','i','n', and 'x'! Thus symbols of this kind must be established with TeX macros like the one shown for the sine function. An author will undoubtedly find the need for constants of this nature. The required TeX macros may be added to the source document itself or preferably to an associated .tdf (or .ldf) file.
2. Basic Forms
The basic forms are the elementary terms and formulas from which the language is generated by substitution. Basic forms result either from definitions, the left side of any definition is automatically a basic form, or from declarations, as needed for primitive forms for example. It must be noted that some definitions are generated by definitional schemes, such as are needed to govern removal of parentheses from infix formulas.
ProofCheck's grammar does not accomodate contextual definition. For example one cannot define addition of classes [x] by defining ([x] + [y]). Here the expression ([x] + [y]) is a composite involving distinct basic forms (A + B) and [x]. These need to be defined separately. Similarly the commonly used definition of limit as ((limit x f(x) = L) if and only if For every epsilon, etc.) is contextual and not admissable. The left side contains previously defined basic forms for equality, (A = B), and functional evaluation, f(x). To define the limit as the number L having such and such a property one can use a definite description.
a. The Defining Forms
It is required that definitions of terms take the form
(pq)
where the term definor has been already established in the .tdf (or .ldf) file with a declaration
%term_definor:and that definitions of formulas take the form
(xy)
where the formula definor has been established with a declaration
%formula_definor:
b. Undefined Form Declarations
When a basic form is needed and not defined, either because it is truly primitive such as '(x \in y)' or just a form whose definition is inconvenient, it may be delcared using a ProofCheck declaration:
%undefined_term: <new-term>Undefined basic formulas are added using
%undefined_formula: <new-formula>For example a development of axiomatic set theory should contain the declaration:
%undefined_formula: (x \in y)where of course (x \in y) appears as
The undefined formula declarations should include two for the two defining forms.
c. Schematic Expressions
A schematic expression is a schemator of arity-n followed by n not necessarily distinct (object) variables. A schemic form is a schemator of arity-n followed by n distinct (object) variables. A schemic term is a schemic form whose initial symbol is a term schemator. A schemic formula is a schemic form whose initial symbol is a formula schemator. Thus a schemic form is either a schemic term or a schemic formula.
d. Basic Terms and Formulas
A basic form is either the left side of a definition or an expression explicitly declared to be an undefined term or formula. A basic term is either the left side of a term defining definition or an expression explicitly declared to be an undefined term. A basic formula is either the left side of a formula defining definition or an expression explicitly declared to be an undefined formula. Thus a basic form is either a basic term or a basic formula.
e. Rules for Basic Forms - Symbol Occurrences
Rules for the Occurrences of Symbols in a Basic Form:
BF1. Every basic form begins with a constant.A constant which occurs as the initial symbol of some basic form is called an introductor. We have that the left parenthesis is an introductor. The following rules restrict the occurrence of variables in basic forms.
BF2. No sentential variable occurs more than once.
BF3. No schemator appears more than once.
- BF4. Every occurrence of a schemator is as the initial
- symbol of a schematic expression.
Although one might naively expect that each variable should occur at most once, Morse's handling of bound variables renders that restriction undesirable for object variables.
BF5. An object variable that occurs at most once occurs in no schematic expression.
- BF6. An object variable that occurs more than once, occurs in some
- schematic expression and at least once not within a schematic expression.
Morse did not use rule BF6. An alternate rule observed by Morse is the following:
- BF6'. An object variable that occurs more than once, occurs in every
- schematic expression and exactly once not within a schematic expression.
A variable is free in a basic form if and only if it occurs in it at most once. A variable is indicial in a basic form if and only if it occurs in it more than once. The schematic expressions in which an indicial variable occurs constitute the scope of that variable. The most common basic forms contain no indicial variables at all. Basic forms with more than one indicial variable are uncommon. For example in
'x' is indicial and 'A' is free and lies outside the scope of 'x'. In
'x' and 'y' are free and there are no indicial variables.
BF6' prohibits repeated indicial variables as in:
Such forms, although of dubious value, are required by context-freeness, at least assuming that multiple indicial variables are allowed as in:
One advantage of BF6 over rule BF6' is that it allows for the description of the resulting terms and formulas by means of a context-free grammar.
A basic form is strict if each of its indicial variable occurs exactly once not within a schematic expression. Imposing BF6' would require all basic forms to be strict.
There are more rules for basic forms. These rules apply to the set of basic forms as a whole. Their statement depends on some additional terminology.
f. Signatures and Variants
The signature of a basic form is the expression obtained by replacing:
- Each sentential variable by F,
- Each variable occurring just once by T,
- Each schematic expression by F or T according as its initial symbol is a formula schemator or a term schemator,
- Each remaining variable by V.
We note that the signature of a basic form contains no variables, only constants and the three symbols T, F, and V which will be used as grammatical non-terminal symbols.
The signature of a schematic expression is obtained by replacing each variable by T. If its initial symbol is a term schemator it is called a schemic term signature and if its initial symbol is a formula schemator it is called a schemic formula signature.
A final signature is obtained from a signature by replacing each V by T.
The expression A is a variant of the expression B if and only if A can be obtained from B by replacing variables by variables and vice versa.
g. Terms and Formulas
The terms and formulas can be specified using formal grammars or by using elementary recursion.
i) Using context free grammars:
Three non-terminal symbols are needed: T, F, and V.
Let P be the set of the production rules:
T -> b for all signatures b of basic terms and all schemic term signatures b
F -> b for all signatures b of basic formulas and all schemic formula signatures b
T -> V
F -> v for all sentential variables v
V -> v for all object variables v
Let S, the set of terminal symbols, be the set of variables of all four kinds and all constants occurring in these production rules.
We then have the context free grammars:
({T,F,V}, S, P, T)which generates the terms and:
({T,F,V}, S, P, F)which generates the formulas.
ii) Alternate formulation
Without using the terminology of formal grammars and signatures we can define the sets of terms and formulas as follows:
- Object variables, basic terms and schematic expressions whose initial symbol is a term schemator are terms.
- Sentential variables, basic formulas and schematic formula expressions whose initial symbol is a formula schemator are formulas.
- If B is a basic term and b is object variable occuring in B just once, or B is a schematic expression whose initial symbol is a term schemator, and b is replaced in B by a term, then the result is a term.
- If B is a basic formula and b is object variable occuring in B just once, or B is a schematic expression whose initial symbol is a formula schemator, and b is replaced in B by a term, then the result is a formula.
- If B is a basic term and b is sentential variable occuring in B, b is replaced in B by a formula, then the result is a term.
- If B is a basic formula and b is sentential variable occuring in B, and b is replaced in B by a formula, then the result is a formula.
- If B is a basic term and b is a schematic expression occurring in B then the result of replacing b by a term or formula, a term if the initial symbol of B is a term schemator, a formula if the initial symbol of B is a formula schemator, is a term.
- If B is a basic formula and b is a schematic expression occurring in B then the result of replacing b by a term or formula, a term if the initial symbol of B is a term schemator, a formula if the initial symbol of B is a formula schemator, is a formula.
- Any variant of a term is a term.
- Any variant of a formula is a formula.
h. Rules for the Set of Basic Forms
The next four rules help to establish that the set of terms and formulas is unambiguous.
BF7. No basic form is both a basic term and a basic formula.
BF8. If basic forms B and B' are variants then B and B' are identical.
The next rule is needed to show that no term or formula can be an initial segment of any other term or formula.
BF9. If basic forms B and B' are basic forms and S and S' are the final signatures of B and B' respectively and S is an initial segment of S' then B and B' are identical.Basic forms B and B' clash if and if letting S be the final signature of B and S' be the final signature of B' there is a common initial segment u of S and of S' such that u is followed in S by an introductor and u is followed in S' by T or F.
For example if the following three expressions were basic forms
the first would clash with both of the other two which on the other hand would not clash with each other.
BF10. If B and B' are basic forms then B and B' do not clash.A basic form A subsumes subsumes B if A is B or B can be obtained from A by replacing index variables of A by index variables of A.
In order to get the context-free property of the grammar it is required that
- BF11. B is a variant of a basic form if and only if there is
- a strict basic form C such that C subsumes some variant B' of B.
For example, BF11 guarantees that all of the following are variants of some basic form if any one of them is.
Note that no two of these expressions are variants each other, and only the first is strict.
i. Rules for Definitions
If L and R are the left and right sides of some definition then then
DF1. Every object variable is bound in L if and only if it is bound in R.
DF2. Every sentential variable occurs in L if and only if it occurs in R.
DF3. Every schemator occurs in L if and only if it occurs in R.
On the set of definitions we require that:
DF4. If L is the left side of both definitions D and D' then D is D'.
j. Definitional Scheme for Infix Operators
Two broad definitional schemes are in effect. The first sets up a mechanism for handling standard infix notational conventions. The second codifies notational conventions that apply to bound variable operators (These two mechanisms constitute the bulk of what Morse called ''Theory of Notation.'')
The first mechanism takes effect following any introductory left parenthesis, in other words any left parenthesis which occurs as the initial symbol of a form and therefore signals a form containing infix operators. There are two declarations associated with infix operators:
i) Precedence Assignment
The first assigns a numerical precedence level to a symbol or to a concatenation of symbols called a nexus:
%set_precedence: <symbol[s]> <number>A symbol whose precedence is defined in this way becomes an infix operator. Symbols whose precedence has been defined may then be grouped to form a nexus whose precedence may be set to a value not dependent on single symbol precedence values. For example one could set the precedence of '< =', a two symbol nexus with:
%set_precedence: <= 17Provided that the precedence of the two constituent symbols has already been declared, as with e.g.:
%set_precedence: < 7
%set_precedence: = 4
There is no necessary relation between the assigned precedence values.
When the left side of a definition is enclosed in parentheses it is assumed that infix operator notation is being defined. Operators occurring in such a definition must have a precedence assigned.
This declaration may occur in the same file as the definition or better in an included ".tdf" or ".ldf" file.
It is important to keep in mind that these infix operators will parse correctly only when they occur inside at least one set of parentheses. For example the expressions
(x + y = z)
(x \in y \cup z)
parse without difficult as
((x + y) = z)
(x \in (y \cup z))
assuming of course that the precedence of '=' is less than that of '+' and that the precedence of '\in' is less than that of '\cup'.
On the other hand note that because of the lack of outer parentheses, neither
(x + y) = znor
x \in (y \cup z)will be parsed at all.
ii) Checker and Handler Assignment
The result of parsing an infix expression purely on the basis of precedence is an expression compounded of expressions whose infix operators all have the same precedence. These single precedence expressions must be assigned a checker and optionally a handler which performs additional simplifications. The assignment is done with a declaration
%def_precedence: <number> <checker> [<handler>]The parser however does not automatically group operations of equal precedence either to the left or to the right. Repeated and mixed operations of equal precedence are in general left to the user to define.
iii) Available Checkers and Handlers
At present the following checkers are available:
n_arycheck, checks that the expression is of the form
form (x1 + x2 + ... + xn) where all the infix operators
are the same.
mix_check, checks that the expression is of the form
form (x1 + x2 + ... + xn) where the infix operators
may be any operators of the same precedence.
followercheck, checks that the expression is of the
form (x op1 op2 ... opn) where the operators
are followers, like complement and closure in topology.
condelscheck, used to parse if-then-else expressions
using the operators '\cond'' and '\els'.Morse_verbcheck, used when verbs such as < and =
are allowed in succession as in
(x1 < x2 = ... < xn)
verbcheck, used when in addition to the use of verbs in succession,
the comma, for the sake of parsing plurals, such as
(x , y , z < A = B)
is given the same precedence as the verbs.
The commas must all come first.
dontcheck, rejects all expressions of that precedence and is
useful for infix operators which occur only as part of some nexus.At present the following handlers are available:
verbexpandIt works in conjunction with verbcheck and parses implied conjunctions and plural forms.
Implied Conjunctions
When more than one verb is used, as in the expression
(x < y = z),it is parsed as a conjunction:
(x < y) and (y = z).Plural Forms
When a verb is preceded by a comma which is in turn preceded by comma separated terms as in the expression
(x,y,z < A),it is parsed as:
(x < A) and (y < A) and (z < A).In order for verbexpand to recognize the infix connector symbols which are verbs they must be declared either individually or by precedence value:
%speechpart: 6 verbIn this case the comma needs to have the same precedence:
%set_precedence: , 6
k. Definitional Scheme for Bound Variable Operators
Quantifiers are the archtypical bound variable operators. In the Polish tradition other bound operators variables are given syntactically similar treatment. This means that the set forming operator, the summation operator, indexed unions and intersections, etc. all become syntactic analogs of the quantifiers. Bound variable operators that are handled in this way are, following Morse, called notarians. It is not required, however, that all bound variables occur in forms introduced by a notarian. Other bound variable forms do exist. But the syntactic variation made available by implementing a definition using a notarian is almost always a decisive argument in its favor.
Whether a form containing a index variable is notarian form or not depends on its definition.
Syntactic variation for notarians can be illustrated in the case of the universal quantifier.
So just as we can write
\Each x (x < B)we can also write:
\Each x < A (x < B)or:
\Each x < A;(x \ne y) (x < B)or:
\Each x,y< A (x + y < B)or:
\Each x,y< A; (y > x) (x + y < B)
i) Formula Notarians
New bound variable operators may be introduced as notarians, and thereby get automatically generated variants.
For example to declare that 'Each' be a formula notarian:
%notarian_formula: \Each x ; \pbar x \qbar xIf a bound variable operator indexes a formula, as for example a quantifier, a description, or the set-forming operator, then that operator will be treated by ProofCheck as a notarian if and only if its basic form has the following structure:
<bound-variable-operator> x \pbar x
ii) Term Notarians
If a bound variable operator indexes a term, as for example in summation or indexed union then that operator will be treated by ProofCheck as a notarian if and only if its basic form has the following structure:
<bound-variable-operator> x; \pbar x \ubar xBasic forms containing bound variables are by no means restricted to these very specific forms. However, not to use them means laborious definition of minor syntactic variations. Suppose for example that summation were defined using the form:
\sum x \ubar xIn that case another definition would be needed for
\sum x \in A \ubar xand another for
\sum x \in A \cup B \ubar xetc.
For example to declare that 'sum' be a term notarian:
%notarian_term: \sum x ; \pbar x \qbar xThis declaration opens the door to all these forms for summation:
For notarians which index terms (not formulas) there is also a deferred scope form as in:
\bigcup (x \cap y)\ls x \in A \rswhere \ls and \rs stand for left scope and right scope brackets.
5. Proof Syntax
a. Free, Indicial and Bound Variables
A variable is free in a basic form if it occurs no more than once. It is free in other words if it occurs in none of the schematic expressions of the basic form.
A variable is free in a term or formula if every occurrence is a free occurrence. This is the case if it never occurs in a location occupied by a V in the signature of a basic form. In particular a variable that does not occur at all is free.
A basic fact noted by Morse is the following: If a variable v is free in a term or formula F and v is replaced by a term or formula G then the result is a term or formula in which any variable x is free if and only if it is free in both F and G.
A variable is indicial in a basic form if it occurs more than once. It is indicial in other words if it occurs in at least one schematic expression of the basic form.
If a term or formula is obtained from a basic form B by replacing schematic expressions and sentential and free variables by terms and formulas then a variable x is indicial in the result if and only if x is indicial in B.
For example 'x' is indicial the first four of the following but not in the fifth:
A variable is bound in a basic form if it does not occur exactly once.
If a term or formula is obtained from a basic form B by replacing schematic expressions and sentential and free variables u1, u2, ... un by terms and formulas be F1, F2, ... Fn and then a variable x is bound in the result if and only if
x is bound in F1, or u1 is a schematic expression and x occurs in u1 and
x is bound in F2, or u2 is a schematic expression and x occurs in u2 and ...
x is bound in Fn, or un is a schematic expression and x occurs in un .
In other words a variable is bound in a term or formula if every occurrence is a bound occurrence. In the five expressions above 'x' is bound in all but the third.
b. Substitution Rules of Inference
Rules of inference require the formulation of syntactic conditions. Strengthening the rules cannot be done without sacrificing to some extent the simplicity of these conditions. The first rule below requires only the notion of freeness (see i above). The second rule requires no special condition. A schematic rule, unlike those given below, can be given using very simple conditions, but these weaken the rule unacceptably.
To state the schematic substitution rules below let us first suppose that we seek to substitute a term or formula F for a schematic expression u in a term or formula T. We require that
- The variables of u be distinct and may not occur in T.
- Every variable be either free in F or bound in F.
- Every variable not bound in F be free in T.
- Every variable not bound in T be free in F.
If these conditions are met then let us define the schematic substitution of F for u in T recursively as follows:
- If the initial symbol of T be that of u then letting the terms of T which follow the initial symbol be T1, T2, ... Tn and the distinct variables of u be z1, z2 , ... zn and then the result of the schematic substitution of F for u in T is the result of replacing z1, z2 , ... zn in F by be the T1', T2', ... Tn' obtained by schematically substituting u for F in T1, T2, ... Tn.
- If T is obtained from a term or formula S in which the initial symbol of u does not occur by replacing free object variables v1, v2 , ... vm in S by terms u1, u2 , ... um whose initial symbol is that of u then the result of the schematic substitution of F for u in T is the T' obtained from S by replacing v1, v2 , ... vm in S by the terms T1', T2', ... Tm' in S by terms obtained from u1, u2 , ... um by schematically substituting u by F.
As an example of schematic substitution suppose that T is
and that u is '\ubar z' and F is '(z + 1)' then the result of schematically substituting F for u in T is
To state the indicial substitution rule below we use constituent replacement. T' is obtained from T by a constituent replacement of F by F' if there is a formula S containing a free variable v if F is a term or sentential variable v if F is a formula, such that T is obtained from S by replacing v by F. T' is then obtained by constituent replacement of F' by F is T' is obtained from S by replacing v by F'. T' is obtained from T by indicial substitution of y for x if
- x is indicial in F
- y a variable that is not indicial in F and does not appear in the scope of x in F
- F' is obtained from F by replacing x by y
- T' is obtained from T by constituent replacment of F by F'
As an example of indicial subsitution suppose that T is
and that x is 'y' and y is 'z' then the result of indicially replacing x by y is:
Inference rules which warrant the inference of a substitution instance T' of a theorem T vary according to the nature of the substitution and this in turn depends on the nature of the variable in T which is being replaced. In a Morse language we have substitutions for:
Free object variables
If T is a theorem and v is free in T and F is a term and every variable of F is free in T then the T' obtained by replacing v by F in T is a theorem.
Sentential variables
If T is a theorem and v is a sentential variable in T and F is a formula and every variable of F is free in T then the T' obtained by replacing v by F in T is a theorem.
Term schemators
If T is a theorem and u is term whose initial symbol is a term schemator and T' is obtained from T by schematically substituting a term F for u then T' is a theorem.
Formula schemators
If T is a theorem and u is term whose initial symbol is a formula schemator and T' is obtained from T by schematically substituting a formula F for u then T' is a theorem.
Indicial Variables
If T is a theorem and T' is obtained from T by indicial substitution of y for x then T' is a theorem.
In ProofCheck the unifier is responsible for all of these substitutions.
6. Summary
Lists of symbols occurring in the common notions file are here:
You can test expressions here: Online Expression Parser.
G. Unification
Almost all of the work of ProofCheck is done by the unifier.
1. Second order unification
The unifier handles first and second order term and formula variables. First order term variables, ordinary object variables in other words, may occur bound in expressions submitted to the unifier.
2. Variables as Constants
Variables in expressions sent to the unifier must be distinguished according to whether they are subject to substitution in order to achieve unification or whether they are to be treated as constants. Generally speaking the variables in a goal being checked are treated as constants, while those in rules of inference and theorems are not.
3. AC-unification
The unifier is an AC-unifier, in that infix operators whose associative and commutative properties have been stated in theorems stored in the properties file are matched, with these properties allowed for in the unification.
Example
(\pvar \And \qvar \And \rvar) matches (\rvar \And \pvar \And \qvar)In matches between such conjunctions, a sentential variable in one may match with a subset of the conjuncts in the other.
4. Searches Refused
If a rule of inference contains a conjunction (\pvar \And \qvar) where \pvar and \qvar are not in any way distinguished, then a search for a match of this conjunction with n conjuncts would require searching over all subsets of these n conjuncts. These searches are refused by the unifier. No match will be found. Rules of inference which entail such searches are effectively ignored. The unifier is therefore incomplete as a matter of policy.
Searches in analogous situations are also refused.
Rules of inference need to be stated without the use of unnecessary variables.
H. Multi-Line Note Processing
A multi-line note is a note which occupies more than one line in the source file and at least one of its continuation lines begins with a transitive operator.
1. Transitive Operators
An operator is a transitive operator if there is a theorem stating its transitive property stored in the properties file. By default the properties file is properties.tex. According to this file the implication sign, for example, is a transitive operator.
Only infix operators can be recognized as transitive.
2. Parsing
A multi-line note is broken into subgoals called delta goals which are combined to form sigma goals.
Example
(p \And q \c x < y
< z
< w)
The first line is parsed as:
(p \And q \c x < y)This goal is referred to as a delta goal. The second line parses into two goals, a delta goal:
(p \And q \c y < z)and a sigma goal:
(p \And q \c x < z)The third line also parses into a delta goal:
(p \And q \c z < w)and a sigma goal:
(p \And q \c x < w)When a multi-line note is invoked later in a proof it is the last sigma goal which is referred to.
3. Checking
Steps in a multi-line proof require on the average two goals to be checked instead of just one. A multi-line note with n steps produces (2n - 1) goals.
Justifications on each line of a multi-line proof are attached to the delta goals. More abstract transitivity theorems, in particular those in the properties file are invoked in order to check the sigma goals. The search for these is an exception to the general rule that ProofCheck does not search for theorems.